excel拖动排列步骤如下：1.我在EXCEL中输入以下数字，如图：2.现在我要想复制“1”，则拖动单元格A1，但此该你会发现，在下拖动下方有个方框，如图：3.上步出现的情况便是以顺序的方式出现，但你只需要点动那个右下方的方框，选择“复制单元格”即可......
Excel解多元一次方程组的几种方法
Excel教程
2021-11-13 11:33:21
本文列出了在Excel中解多元一次方程组的三种方法：矩阵解法、用克莱姆法则和用规划求解的方法，供参考。单击右侧链接打开示例文件下载页面：示例文件。
方法一：矩阵解法
原理：对于由n个未知数，n个方程组成的多元一次方程组：
写成矩阵形式为Ax=b，其中A为系数n*n方阵，x为n个变量构成列向量，b为n个常数项构成列向量。当它的系数矩阵可逆，或者说对应的行列式|A|不等于0的时候，由Ax=b可得：x=b*A^(-1) ，A^(-1)为A的逆矩阵。
利用Excel提供的MDETERM、MINVERSE和MMULT等函数即可求解多元一次方程组。MDETERM函数返回一个数组的矩阵行列式的值，可用其判断矩阵是否可逆；MINVERSE函数返回矩阵的逆矩阵；MMULT函数返回两个数组的矩阵乘积。有关MMULT函数的用法可参考《用公式进行多条件求和》一文中的方法三。
示例及步骤：
假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
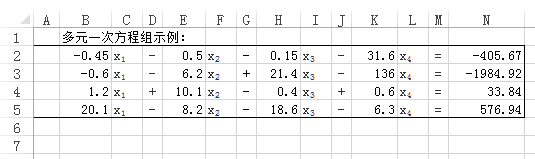
在P2:S5区域用公式得到其系数矩阵，T2:T5的返回值为常数项向量。如P2单元格中的公式为：
=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),COLUMN(A1)*3-3)="-",-1,1)
由于“=MDETERM(P2:S5)”的值不等于“0”，可知系数矩阵可逆。选择某列中的四个连续单元格，如Q11:Q14，输入数组公式：
=MMULT(MINVERSE(P2:S5),T2:T5)
公式输入完毕按Ctrl+Shift+Enter结束，即可在Q11:Q14得到方程组的解。
方法二：用克莱姆法则
原理：参考克莱姆法则。
示例及步骤：
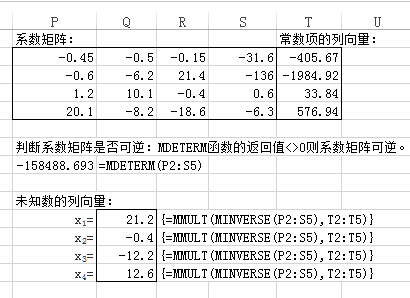
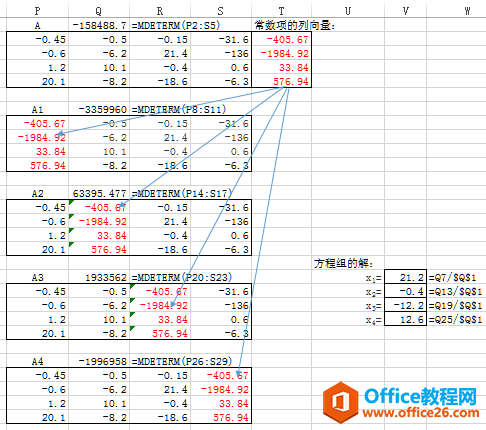
对于上述四元一次方程组，复制P2:S5区域，将其粘贴到其他区域，如本例有4个未知数，用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。然后复制T2:T5常数项的列向量，用“选择性粘贴——粘贴链接”的方法分别将其粘贴到上述四个区域中的各列，依次得到矩阵A1、A2、A3、A4，再用MDETERM函数计算各矩阵行列式的值，分别除以系数矩阵A的行列式的值，即可得到方程组的解。
方法三：用规划求解
原理：规划求解是Excel中的一种加载项，是一种模拟分析工具，它通过调整可变单元格的值来查找满足所设定条件的最优值。
示例及步骤：
以上述四元一次方程组为例，在Excel 2013中的操作步骤如下。
1.加载“规划求解加载项”。如果已加载该加载项可忽略次步。依次单击“文件→选项→加载项”，在对话框的底部“管理”的右侧单击“转到”按钮，弹出“加载宏”对话框，勾选“规划求解加载项”后确定。Excel会在“数据”选项卡中添加“分析”组及“规划求解”按钮。
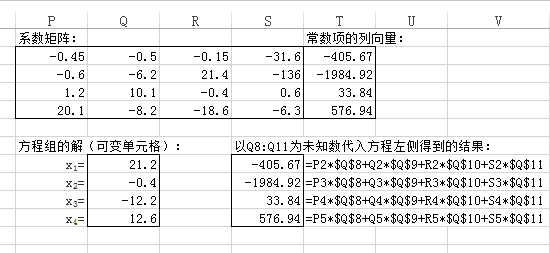
2.设置公式，本例以Q8:Q11为可变单元格，规划求解的结果将在该区域产生。在S8:S11区域设置公式，即以Q8:Q11为未知数代入方程左侧。如S8中的公式：
=P2*$Q$8+Q2*$Q$9+R2*$Q$10+S2*$Q$11
3.设置“规划求解”参数。在“数据”选项卡的“分析”组中单击“规划求解”按钮，弹出“规划求解参数”对话框，进行如下设置：
①设置“通过更改可变单元格”为Q8:Q11；
②在“遵循约束”下添加约束条件。单击“添加”按钮，弹出“添加约束”对话框，将“单元格引用”设置为S8单元格，将“约束”设置为T2单元格后确定，这样就添加了一个约束：S8=T2。
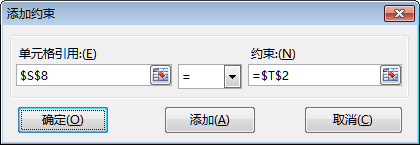
用同样的方法添加其他几个约束：S9=T3、S10=T4和S11=T5；
③取消勾选“使无约束变量为负数”选项。
④选择求解方法为“单纯线性规划”。
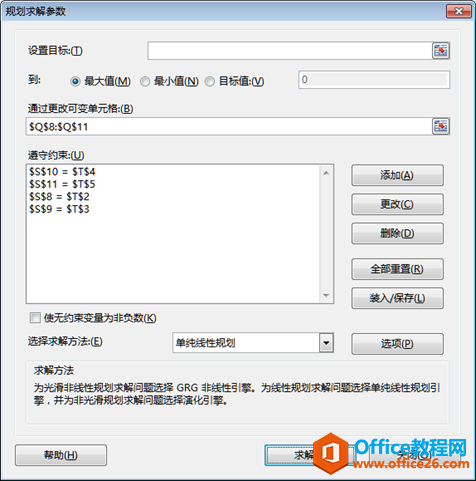
4.单击“求解”按钮，Excel将进行求解。本例很快弹出下面的“规划求解结果”对话框。
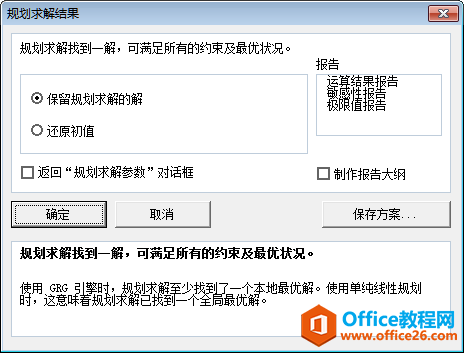
单击“确定”即可在Q8:Q11得到方程的解。
上一篇：利用excel如何快速制作标签 下一篇：Excel数据验证实现实例教程
相关文章