怎样利用几何画板求曲线弧长

几何画板 2021-09-24 09:15:45

直角坐标情形下设函数在区间上具有一阶连续的导数，由此计算曲线的长度。那么怎样用几何画板求曲线弧长呢？下面将举例讲解求曲线弧长的方法。

比如求函数f(x)=x3-3x+3在递减区间上的曲线弧长，具体的操作步骤如下：

步骤一先画出它的图象。单击菜单栏上的“绘图”命令，选择“绘制新函数”选项，输入函数解析式，单击“确定”。

执行“绘图”——“绘制新函数”画出函数图像示例

步骤二求出它的递减区间。求函数的导数，f′(x)=3x2-3=3（x2-1），显然当x<-1或x>1时，f′(x)>0；而当-1≤x≤1时，f′(x) ≤0，所以递减区间为[-1，1]。

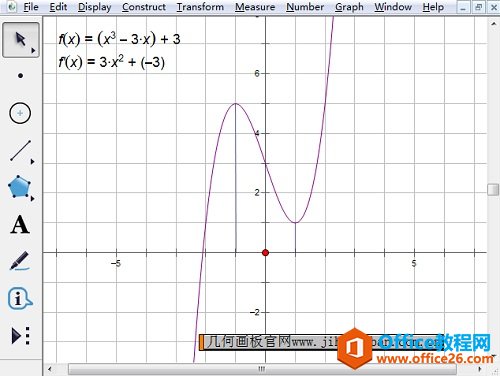
利用导函数求函数的递减区间示例

步骤三算出端点的纵坐标。选择“度量”——“计算”命令，单击函数解析式，输入自变量的值，单击“确定”。先后算出f（-1）=5，f（1）=1。

执行“度量”——“计算”算出端点的纵坐标示例

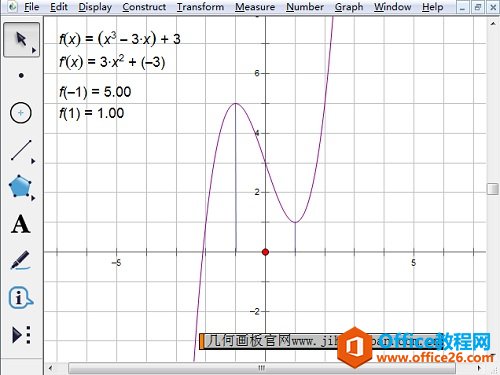
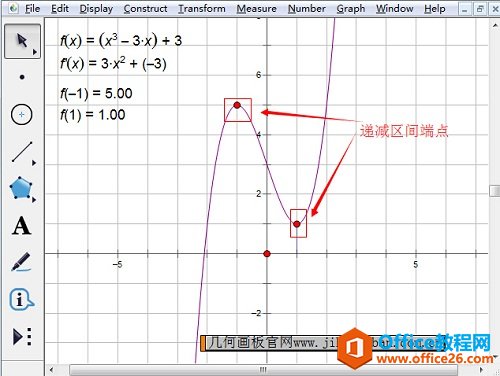
步骤四画出递减区间的两个端点。单击“绘图”菜单，选择“绘制点”，输入坐标（-1，5），单击绘制；再输入坐标（1，1），单击绘制，然后点完成。这样区间端点就画出来了。

画出递减区间的两个端点示例

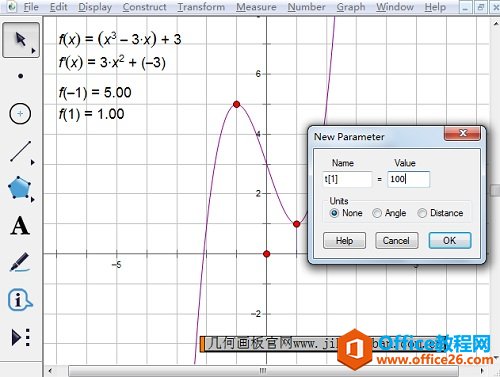
步骤五新建参数。单击“绘图”，选择“新建参数”，新建参数t1=100，单击“确定”。

执行“绘图”——“新建参数”新建参数t1示例

步骤六选择自定义工具。单击自定义工具，选择“函数工具”——弧长，如下图所示。

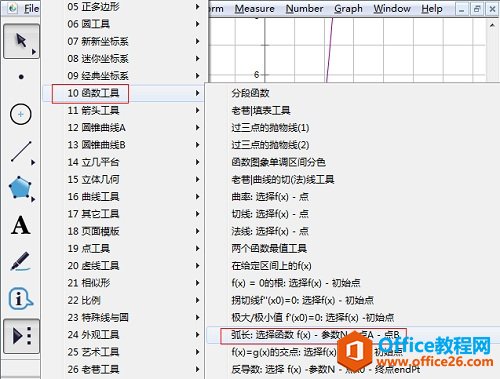
在自定义工具下选择求弧长的函数工具

步骤七计算弧长，注意操作顺序。单击函数解析式，再单击参数t1，然后移动鼠标，对准递减区间的左端点单击一下；继续移动鼠标，对齐右端点时单击一下。这时，弧长数值就显示出来了。

在几何画板中计算弧长示例

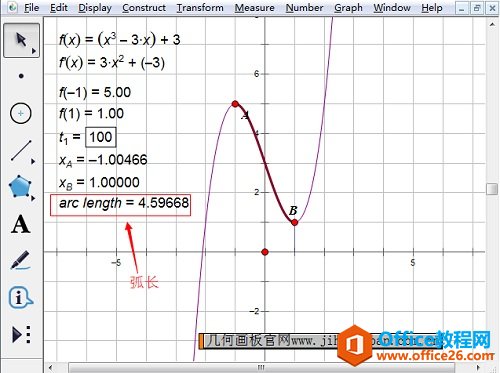
注意：这步严格要求对准端点，怎么看对准了没有呢？一是看颜色，点周围出现浅绿色光环，二是看数值，单击时显示的数值和我们求出的端点横坐标相同，这就说明对准了。

以上给大家举例讲解了用几何画板求曲线弧长的方法，运用了几何画板求导函数和自定义工具下的函数工具，大家参照教程多多练习，即可熟练掌握。