几何画板中如何从结论出发画几何图形

几何画板 2021-09-23 10:01:46

若要证明的命题的逆命题也成立，则可以从结论出发画出几何图形。几何画板是一个非常优秀的CAI工具，将其应用于课堂教学，必将发挥重要的作用。在前面的教程中，我们学习了利用几何画板按已知条件画几何图形的方法，当然，几何画板中也可以实现从结论出发，画出几何图形，下面我们就通过实例来加以说明。

之前教程我们举例的命题是：已知：梯形ABCD中，AD∥BC，AB=AD+BC，E是CD的中点。求证：AE、BE分别平分∠BAD、∠ABC。

该命题的逆命题是：在梯形ABCD中，AD∥BC，∠DAB和∠CBA的平分线交于点E，点E恰好在腰CD上。则：AB=AD+BC，E是CD的中点。

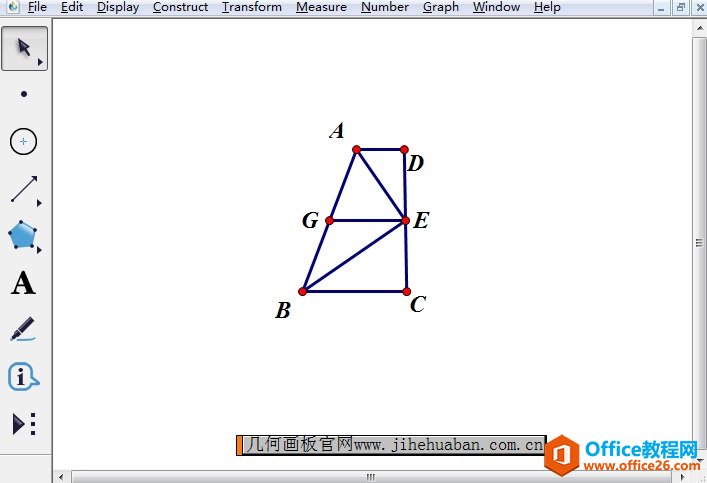
显然，我们可以得知∠AEB=90°。如下图，设线段AB的中点是点G，连结EG，则AG=EG，即：∠AEG=∠EAG=∠EAD。所以AD∥EG，因此，CE=DE，AD+BC=2EG=AB。

在几何画板中画图验证结论示例

由于逆命题是真命题，所以我们可以命题的结论出发画出符合题意的几何图形，画图步骤如下：

步骤一画出腰AB和两底所在的射线。使用“点工具”在画板空白区域任意画两点，使用“射线工具”过两点分别画射线，如下图所示。

在几何画板中画梯形的腰和底边射线示例

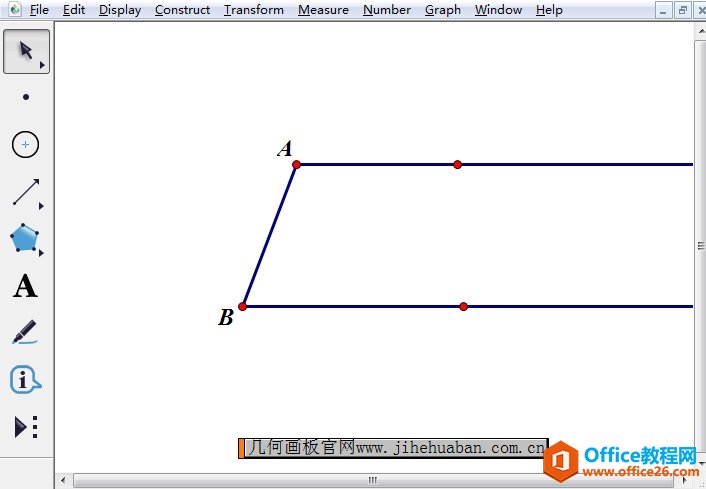
步骤二作∠A和∠B的角平分线，交于点E。依次选中∠A和∠B，执行“构造”——“角平分线”命令，构造出角平分线，如下图所示。

在几何画板中画∠A和∠B的角平分线示例

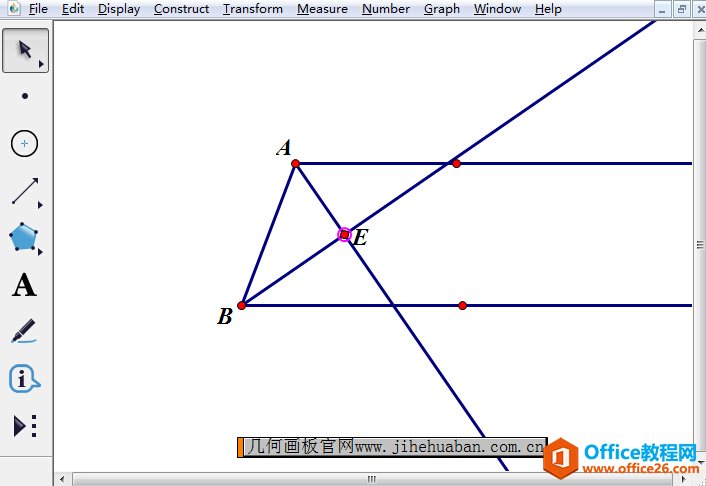
步骤三在一底所在的射线上任取一点C，选择“线段工具”过点E作射线CE，交另一底所在的射线于点D，如下图所示。

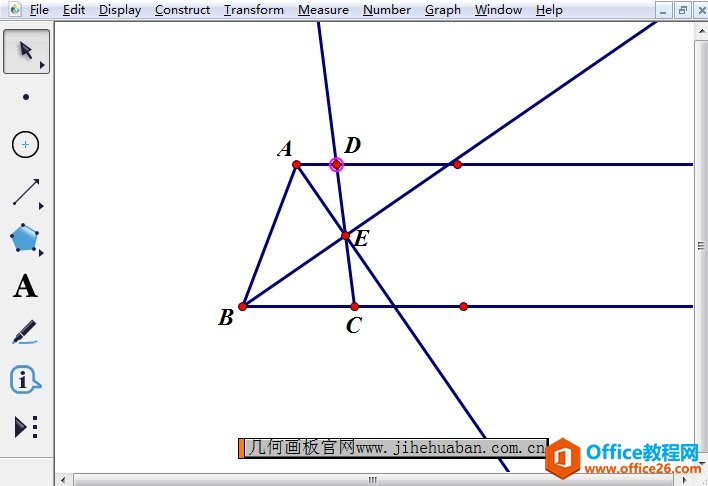
在几何画板中画射线CE示例

步骤四连结相关线段，并将作图过程中的辅助图形隐藏，即可得到符合题意的图形。

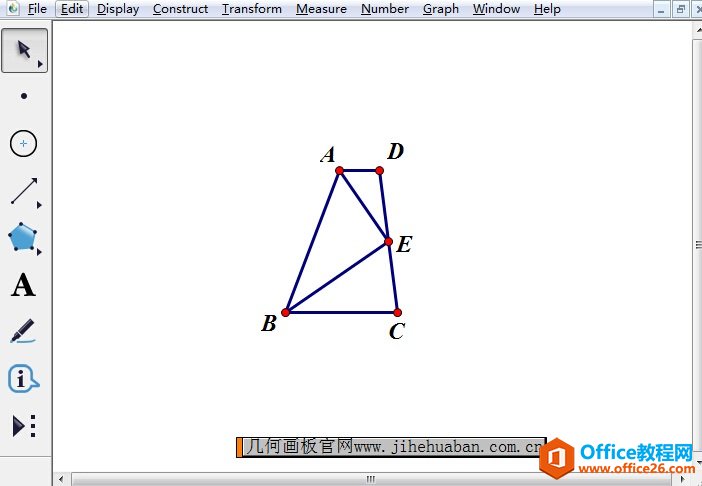
在几何画板中画射线CE示例

从以上例题可以看出，平面几何作图问题通常可以化归为确定某些点的位置的问题，而一个点的位置往往是由两个条件决定的。

以上教程教大家在几何画板中从结论出发画几何图形的方法，数学中的命题证明题都是可以有逆命题的，大家可以根据教程多练习练习，掌握几何画板画几何图形的奥秘。